Important libraries
class: middle
Import Data: Paris paintings
pp <- read_csv("paris-paintings.csv", na = c("n/a", "", "NA"))
pp <- read_csv(file.choose())- Number of observations: 3393
- Number of variables: 61
Goal: Predict height from width
\[\widehat{height}_{i} = \beta_0 + \beta_1 \times width_{i}\]
## `geom_smooth()` using formula 'y ~ x'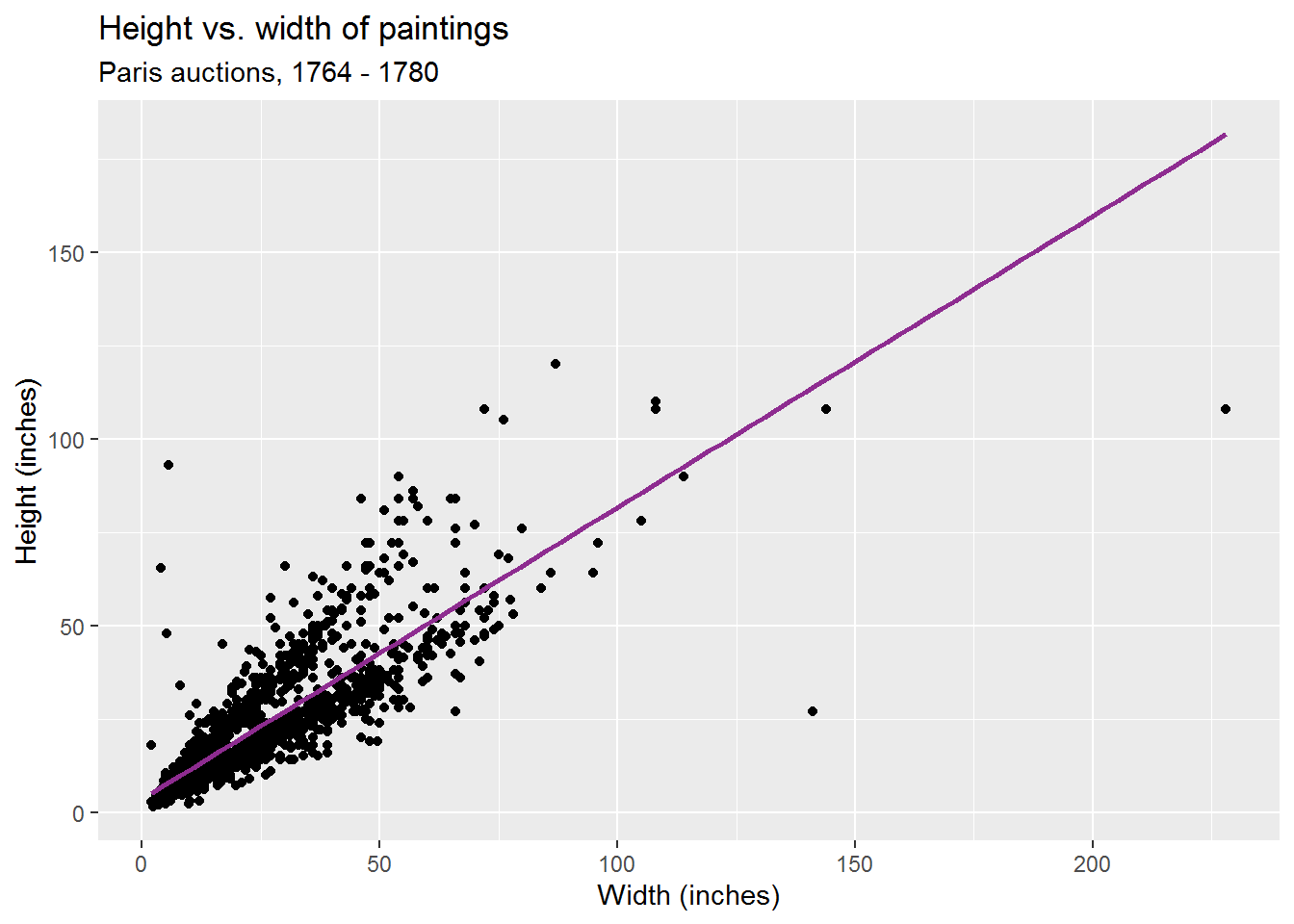

Step 1: Specify model
linear_reg()## Linear Regression Model Specification (regression)| ## Step 2: Set model fitting engine |
r linear_reg() %>% set_engine("lm") # lm: linear model |
## Linear Regression Model Specification (regression) ## ## Computational engine: lm |
Step 3: Fit model & estimate parameters
… using formula syntax
linear_reg() %>%
set_engine("lm") %>%
fit(Height_in ~ Width_in, data = pp)## parsnip model object
##
## Fit time: 0ms
##
## Call:
## stats::lm(formula = Height_in ~ Width_in, data = data)
##
## Coefficients:
## (Intercept) Width_in
## 3.6214 0.7808A closer look at model output
## parsnip model object
##
## Fit time: 0ms
##
## Call:
## stats::lm(formula = Height_in ~ Width_in, data = data)
##
## Coefficients:
## (Intercept) Width_in
## 3.6214 0.7808.large[ \[\widehat{height}_{i} = 3.6214 + 0.7808 \times width_{i}\]]
A tidy look at model output
linear_reg() %>%
set_engine("lm") %>%
fit(Height_in ~ Width_in, data = pp) %>%
tidy()## # A tibble: 2 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 3.62 0.254 14.3 8.82e-45
## 2 Width_in 0.781 0.00950 82.1 0.large[ \[\widehat{height}_{i} = 3.62 + 0.781 \times width_{i}\]]
Slope and intercept
.large[ \[\widehat{height}_{i} = 3.62 + 0.781 \times width_{i}\]]
–
- Slope: For each additional inch the painting is wider, the height is expected to be higher, on average, by 0.781 inches.
| - Intercept: Paintings that are 0 inches wide are expected to be 3.62 inches high, on average. (Does this make sense?) |
Correlation does not imply causation
Remember this when interpreting model coefficients

.footnote[ Source: XKCD, Cell phones]
class: middle
Parameter estimation
Linear model with a single predictor
- We’re interested in \(\beta_0\) (population parameter for the intercept) and \(\beta_1\) (population parameter for the slope) in the following model:
\[\hat{y}_{i} = \beta_0 + \beta_1~x_{i}\]
| - Tough luck, you can’t have them… |
|---|
| - So we use sample statistics to estimate them: |
| \[\hat{y}_{i} = b_0 + b_1~x_{i}\] |
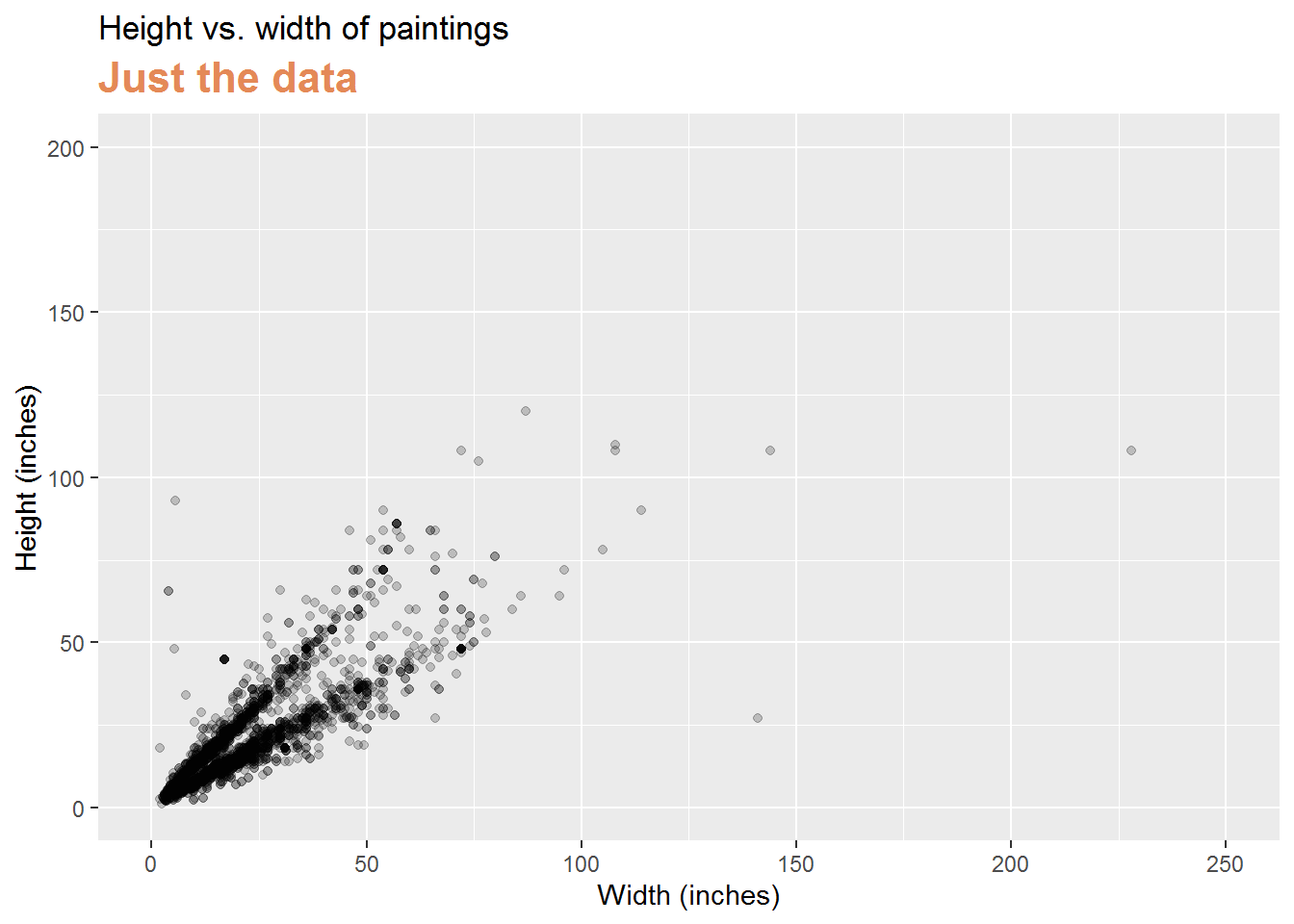
Least squares regression
- The regression line minimizes the sum of squared residuals.
| - If \(e_i = y_i - \hat{y}_i\), then, the regression line minimizes \(\sum_{i = 1}^n e_i^2\). |
Visualizing residuals
Visualizing residuals (cont.)
## `geom_smooth()` using formula 'y ~ x'
Visualizing residuals (cont.)
## `geom_smooth()` using formula 'y ~ x'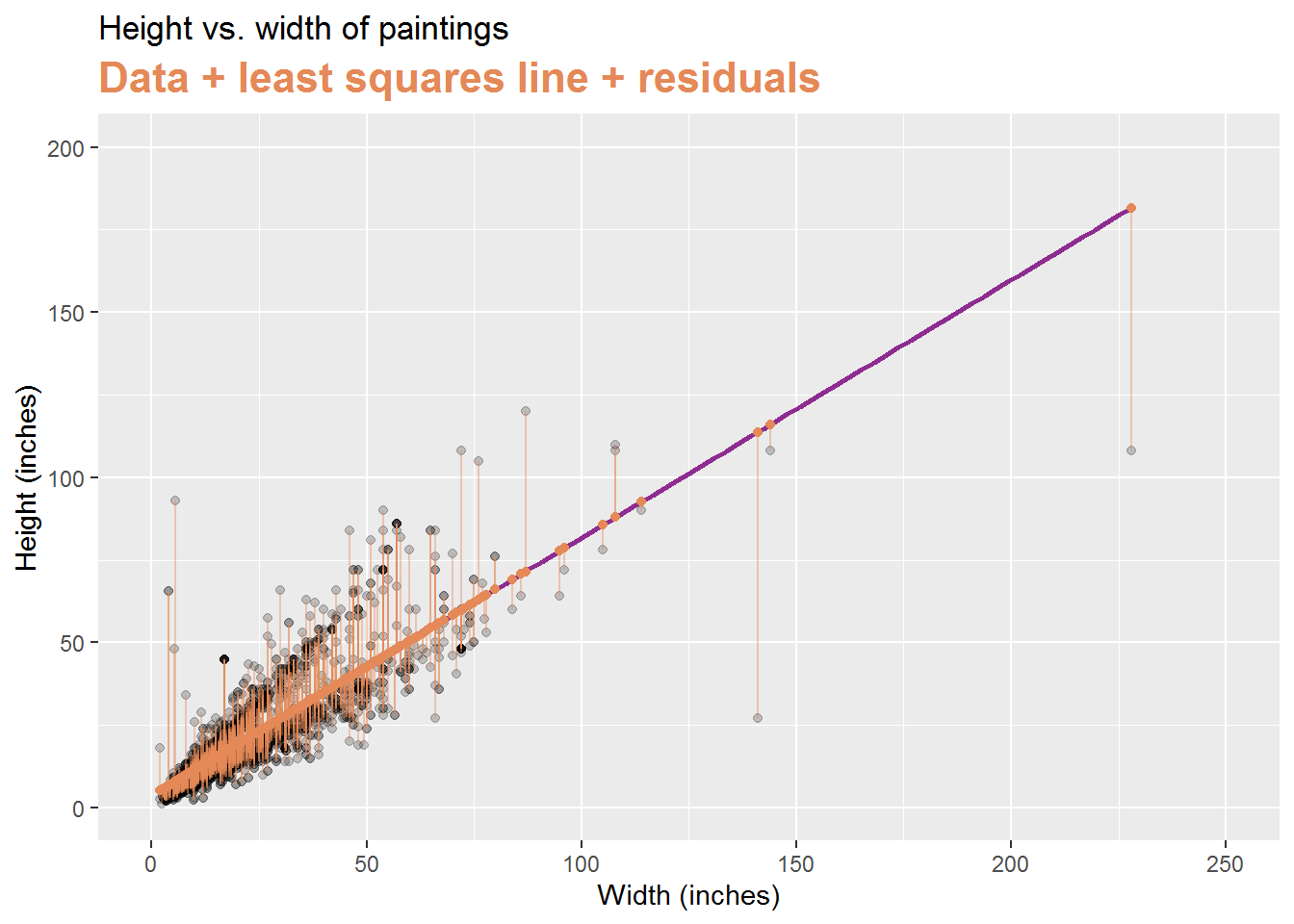
Properties of least squares regression
- The regression line goes through the center of mass point, the coordinates corresponding to average \(x\) and average \(y\), \((\bar{x}, \bar{y})\):
\[\bar{y} = b_0 + b_1 \bar{x} ~ \rightarrow ~ b_0 = \bar{y} - b_1 \bar{x}\]
| - The slope has the same sign as the correlation coefficient: \(b_1 = r \frac{s_y}{s_x}\) |
|---|
| - The sum of the residuals is zero: \(\sum_{i = 1}^n e_i = 0\) |
- The residuals and \(x\) values are uncorrelated
class: middle
Models with categorical explanatory variables
Categorical predictor with 2 levels
.pull-left-narrow[ .small[
## # A tibble: 3,393 x 3
## name Height_in landsALL
## <chr> <dbl> <dbl>
## 1 L1764-2 37 0
## 2 L1764-3 18 0
## 3 L1764-4 13 1
## 4 L1764-5a 14 1
## 5 L1764-5b 14 1
## 6 L1764-6 7 0
## 7 L1764-7a 6 0
## 8 L1764-7b 6 0
## 9 L1764-8 15 0
## 10 L1764-9a 9 0
## 11 L1764-9b 9 0
## 12 L1764-10a 16 1
## 13 L1764-10b 16 1
## 14 L1764-10c 16 1
## 15 L1764-11 20 0
## 16 L1764-12a 14 1
## 17 L1764-12b 14 1
## 18 L1764-13a 15 1
## 19 L1764-13b 15 1
## 20 L1764-14 37 0
## # ... with 3,373 more rows]
]
.pull-right-wide[
- landsALL = 0: No landscape features
- landsALL = 1: Some landscape features]
Height & landscape features
linear_reg() %>%
set_engine("lm") %>%
fit(Height_in ~ factor(landsALL), data = pp) %>%
tidy()## # A tibble: 2 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 22.7 0.328 69.1 0
## 2 factor(landsALL)1 -5.65 0.532 -10.6 7.97e-26Height & landscape features
\[\widehat{Height_{in}} = 22.7 - 5.645~landsALL\]
- Slope: Paintings with landscape features are expected, on average, to be 5.645 inches shorter than paintings that without landscape features
- Compares baseline level (
landsALL = 0) to the other level (landsALL = 1)
- Compares baseline level (
- Intercept: Paintings that don’t have landscape features are expected, on average, to be 22.7 inches tall
Relationship between height and school
linear_reg() %>%
set_engine("lm") %>%
fit(Height_in ~ school_pntg, data = pp) %>%
tidy()## # A tibble: 7 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 14.0 10.0 1.40 0.162
## 2 school_pntgD/FL 2.33 10.0 0.232 0.816
## 3 school_pntgF 10.2 10.0 1.02 0.309
## 4 school_pntgG 1.65 11.9 0.139 0.889
## 5 school_pntgI 10.3 10.0 1.02 0.306
## 6 school_pntgS 30.4 11.4 2.68 0.00744
## 7 school_pntgX 2.87 10.3 0.279 0.780Dummy variables
## # A tibble: 7 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 14.0 10.0 1.40 0.162
## 2 school_pntgD/FL 2.33 10.0 0.232 0.816
## 3 school_pntgF 10.2 10.0 1.02 0.309
## 4 school_pntgG 1.65 11.9 0.139 0.889
## 5 school_pntgI 10.3 10.0 1.02 0.306
## 6 school_pntgS 30.4 11.4 2.68 0.00744
## 7 school_pntgX 2.87 10.3 0.279 0.780- When the categorical explanatory variable has many levels, they’re encoded to dummy variables
- Each coefficient describes the expected difference between heights in that particular school compared to the baseline level
Categorical predictor with 3+ levels
.pull-left-wide[| school_pntg | D_FL | F | G | I | S | X |
|---|---|---|---|---|---|---|
| A | 0 | 0 | 0 | 0 | 0 | 0 |
| D/FL | 1 | 0 | 0 | 0 | 0 | 0 |
| F | 0 | 1 | 0 | 0 | 0 | 0 |
| G | 0 | 0 | 1 | 0 | 0 | 0 |
| I | 0 | 0 | 0 | 1 | 0 | 0 |
| S | 0 | 0 | 0 | 0 | 1 | 0 |
| X | 0 | 0 | 0 | 0 | 0 | 1 |
] .pull-right-narrow[ .small[
## # A tibble: 3,393 x 3
## name Height_in school_pntg
## <chr> <dbl> <chr>
## 1 L1764-2 37 F
## 2 L1764-3 18 I
## 3 L1764-4 13 D/FL
## 4 L1764-5a 14 F
## 5 L1764-5b 14 F
## 6 L1764-6 7 I
## 7 L1764-7a 6 F
## 8 L1764-7b 6 F
## 9 L1764-8 15 I
## 10 L1764-9a 9 D/FL
## 11 L1764-9b 9 D/FL
## 12 L1764-10a 16 X
## 13 L1764-10b 16 X
## 14 L1764-10c 16 X
## 15 L1764-11 20 D/FL
## 16 L1764-12a 14 D/FL
## 17 L1764-12b 14 D/FL
## 18 L1764-13a 15 D/FL
## 19 L1764-13b 15 D/FL
## 20 L1764-14 37 F
## # ... with 3,373 more rows] ]
Relationship between height and school
.small[
## # A tibble: 7 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 14.0 10.0 1.40 0.162
## 2 school_pntgD/FL 2.33 10.0 0.232 0.816
## 3 school_pntgF 10.2 10.0 1.02 0.309
## 4 school_pntgG 1.65 11.9 0.139 0.889
## 5 school_pntgI 10.3 10.0 1.02 0.306
## 6 school_pntgS 30.4 11.4 2.68 0.00744
## 7 school_pntgX 2.87 10.3 0.279 0.780- Austrian school (A) paintings are expected, on average, to be 14 inches tall.
- Dutch/Flemish school (D/FL) paintings are expected, on average, to be 2.33 inches taller than Austrian school paintings.
- French school (F) paintings are expected, on average, to be 10.2 inches taller than Austrian school paintings.
- German school (G) paintings are expected, on average, to be 1.65 inches taller than Austrian school paintings.
- Italian school (I) paintings are expected, on average, to be 10.3 inches taller than Austrian school paintings.
- Spanish school (S) paintings are expected, on average, to be 30.4 inches taller than Austrian school paintings.
- Paintings whose school is unknown (X) are expected, on average, to be 2.87 inches taller than Austrian school paintings. ]